blog/content/post/算法题/子序列dp.md

title	description	date	lastmod	slug	categories	tags	math
两字符串系列DP问题归纳	两字符串二维DP系列问题	2025-08-31T21:50:00+08:00	2025-08-31T21:51:00+08:00	子序列dp	算法题	字符串 动态规划 算法	true

约定：记两个字符串s1和s2的长度分别为 m 和 $n$，令vector<vector<int>> dp(m+1, vector<int>(n+1, 0));，dp[i][j] 表示 s1[0..i-1] 和 s2[0..j-1] 的 (最长公共子序列/不同子序列/……) 的 (长度/个数/……)。

最长公共子序列

给定两个字符串 s1 和 s2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

DP公式

dp[i][j]代表的是s1[0..i-1]和s2[0..j-1]的最长公共子序列的长度。注意到这个问题两个字符串地位是完全对称的，所以DP公式中i和j也应当可以互换。

• 如果 $s1[i-1] = s2[j-1]$，则 $dp[i][j] = dp[i-1][j-1] + 1$。
• 如果 $s1[i-1] \ne s2[j-1]$，则 $dp[i][j] = \max(dp[i-1][j], dp[i][j-1])$。

边界条件

$dp[0][j] = 0$，$dp[i][0] = 0$。

最长回文子序列

给你一个字符串 s ，找出其中最长的回文子序列，并返回该子序列的长度。

示例：

输入：s = "bbbab" 输出：4 解释：一个可能的最长回文子序列为 "bbbb" 。

此题可以看做一个字符串和它的逆序字符串的最长公共子序列。

不同的子序列

给你两个字符串 s1 和 s2 ，统计并返回在 s1 的 子序列 中 s2 出现的个数。

示例：

输入：s1 = "rabbbit", s2 = "rabbit" 输出：3 解释： 如下所示, 有 3 种可以从 s1 中得到 s2 的方案。

• rabbbit
• rabbbit
• rabbbit

DP公式

dp[i][j]代表的是s1[0..i-1]的子序列中s2[0..j-1]的个数。

• 如果 $s1[i-1] = s2[j-1]$，则 $dp[i][j] = dp[i-1][j-1] + dp[i-1][j]$。
• 如果 $s1[i-1] \ne s2[j-1]$，则 $dp[i][j] = dp[i-1][j]$。

边界条件

• $dp[0][j] = 0$，1 <= j <= n，表示在空字符串中找到非空字符串，显然不可能。
• $dp[i][0] = 1$，0 <= i <= m，表示在非空字符串中找到空字符串序列，只有一种办法，删除所有字符。

编辑距离

给你两个单词 s1 和 s2， 请返回将 s1 转换成 s2 所使用的最少操作数。你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例：

输入：word1 = "horse", word2 = "ros" 输出：3 解释：

• horse -> rorse (将 'h' 替换为 'r')
• rorse -> rose (删除 'r')
• rose -> ros (删除 'e')

DP公式

dp[i][j]代表的是s1[0..i-1]转换成s2[0..j-1]所使用的最少操作数。注意到这个问题两个字符串地位也是完全对称的，所以DP公式中i和j也应当可以互换。

• 如果 $s1[i-1] = s2[j-1]$，则 $dp[i][j] = dp[i-1][j-1]$。
• 如果 $s1[i-1] \ne s2[j-1]$，则 $dp[i][j] = \min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1$。

边界条件

• $dp[0][j] = j$，0 <= j <= n，表示将空字符串转换成s2[0..j-1]，需要插入 j 个字符。
• $dp[i][0] = i$，0 <= i <= m，表示将s1[0..i-1]转换成空字符串，需要删除 i 个字符。

两个字符串的最小ASCII删除和

给定两个字符串s1 和 s2，返回 使两个字符串相等所需删除字符的 ASCII 值的最小和。

示例:

输入: s1 = "sea", s2 = "eat" 输出: 231 解释: 在 "sea" 中删除 "s" 并将 "s" 的值(115)加入总和。 在 "eat" 中删除 "t" 并将 116 加入总和。 结束时，两个字符串相等，115 + 116 = 231 就是符合条件的最小和。

DP公式

dp[i][j]代表的是s1[0..i-1]和s2[0..j-1]相等所需删除字符的ASCII值的最小和。注意到这个问题两个字符串地位也是完全对称的，所以DP公式中i和j也应当可以互换。

• 如果 $s1[i-1] = s2[j-1]$，则 $dp[i][j] = dp[i-1][j-1]$。
• 如果 $s1[i-1] \ne s2[j-1]$，则 $dp[i][j] = \min(dp[i][j-1]+s2[j-1], dp[i-1][j]+s1[i-1])$。

边界条件

• $dp[i][0]=dp[i-1][0]+s1[i-1]$，0 <= i <= m。
• $dp[0][j]=dp[0][j-1]+s2[j-1]$，0 <= j <= n。

交错字符串

给定三个字符串 s1、s2 和 s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错组成的。

示例：

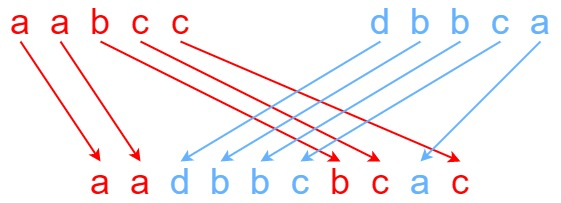
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" 输出：true 解释：s3 可以由 s1 和 s2 交错组成。 s1 = "aabcc" s2 = "dbbca" s3 = "aadbbcbcac" s3 可以由 s1 和 s2 交错组成。

DP公式

dp[i][j]代表的是s1[0..i-1]和s2[0..j-1]能否交错组成s3[0..i+j-1]。注意到这个问题两个字符串地位也是完全对称的，所以DP公式中i和j也应当可以互换。

• 如果 $s1[i-1] = s3[i+j-1]$，则 $dp[i][j] = dp[i-1][j]$。
• 如果 $s2[j-1] = s3[i+j-1]$，则 $dp[i][j] = dp[i][j-1]$。
• 合起来就是 dp[i][j] = (dp[i-1][j] && s1[i-1] == s3[i+j-1]) || (dp[i][j-1] && s2[j-1] == s3[i+j-1])。

边界条件

• dp[0][0] = true，表示空字符串可以交错组成空字符串。
• dp[i][0] = (dp[i-1][0] && s1[i-1] == s3[i-1]) ，1 <= i <= m。
• dp[0][j] = (dp[0][j-1] && s2[j-1] == s3[j-1]) ，1 <= j <= n。
• 必须检查：如果s1.size() + s2.size() != s3.size()，则直接return false。