---
title: 南软/智软2025年开放日机试第1题
description: 图论+并查集问题
date: 2025-07-27T11:59:00+08:00
slug: nju01
# image: helena-hertz-wWZzXlDpMog-unsplash.jpg
categories:
    - 算法题
tags: [
    "图论",
    "并查集",
    "算法",
    "夏令营"
]
math: true
---

# 题目

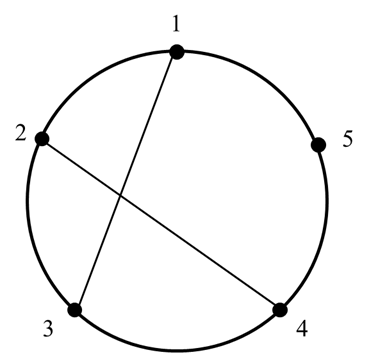
有一个圆上均匀分布着L个点（编号按逆时针顺序依次为1~L）。在这些点中还存在m条弦。如果在圆弧上从一个点走到另一个相邻的点，需要支付1元的费用；但如果通过弦来走（包括交点），则无需支付费用。
例如，如图所示，如果存在弦（1,3）和（2,4），则从点1到点2可以先从1走到两条弦的交点，再从交点走到2，这样就无需收费。请你设计算法，找出某两个点之间最少的交通费。

- 程序的第一行输入三个整数：L、m、q，用空格分隔。
- 接下来输入m行，每行两个整数，表示一条弦。
- 接下来输入q行，每行两个整数，表示q个问题。如“1 2”则表示一个问题，表示点1和2之间的最少交通费。
- 程序的输出为q行，每行为一个问题的答案。

<img src="https://cdn.ember.ac.cn/images/bed/202507271219886.png" width="300">

## 示例输入
```
5 2 1
1 3
2 4
1 2
```

## 示例输出
```
0
```

# 机试情况

南软/智软的夏令营机试是4小时4道题，每题100分，满分400分。4小时内排行榜上此题无人AC，不过有人拿到60-70分。我自己在考场也是没完全做出来，事后思考后才成功做出。

# 解题思路

我们可以自然地把这个问题抽象为一个图，其中包含两种不同代价的边：

- <strong>圆弧边：</strong>连接圆上相邻的两个点，例如点 i 和点 i+1（以及点 L 和点 1）。走这些边需要花费1元，因此它们的边权为 1。
- <strong>免费边：</strong>所有通过弦和弦的交点构成的路径。走这些边无需花费，因此它们的边权为 0。

问题的关键在于，所有通过弦和交点能够互相到达的点，实际上构成了一个“免费交通网络”。网络内的任意两点之间都可以零费用到达。我们可以把这样一个网络视为一个连通分量。

所以我们可以用**并查集** 来高效地处理和合并这些连通分量。

1. **初始化**：将圆上的 `L` 个点每一个都看作一个独立的集合。
2. **合并弦端点**：对于给定的 `m` 条弦，每条弦 `(u, v)` 都意味着 `u` 和 `v` 是零费用连通的。我们将 `u` 和 `v` 所在的集合合并。
3. **合并相交弦**：接下来，我们需要找出所有相交的弦。
   - **如何判断两条弦是否相交？** 假设有两条弦 `(a, b)` 和 `(c, d)`。为了方便判断，我们先将每条弦的端点按编号从小到大排序，即 `u1 = min(a, b), v1 = max(a, b)` 和 `u2 = min(c, d), v2 = max(c, d)`。 这两条弦在圆内相交的充要条件是，它们的端点在圆上是交错排列的。也就是说，必须满足 `u1 < u2 < v1 < v2` 或者 `u2 < u1 < v2 < v1`。
   - 对于每一对相交的弦，例如 `(a, b)` 和 `(c, d)`，它们的所有四个端点 `a, b, c, d` 都应该在同一个零费用连通分量中。我们只需将其中任意一个点（如 `a`）与另一条弦的任意一个点（如 `c`）所在的集合合并即可。

完成以上步骤后，并查集就完整地记录了所有的零费用连通分量。

**第二步：计算两个点之间的最短交通费**

对于每一个查询 `(s, t)`：

1. 首先，我们使用并查集的 `find` 操作检查 `s` 和 `t` 是否在同一个连通分量中。
   - 如果 `find(s) == find(t)`，说明它们在同一个免费交通网络内，可以直接到达，费用为 0。
2. 如果它们不在同一个连通分量中，费用就来自于在圆弧上从一个连通分量“跳”到另一个连通分量的次数。这可以转化为一个在**“分量图”**上的最短路问题。
   - **构建分量图**：图中的每个节点代表一个连通分量。
   - **分量图的边**：如果圆弧上相邻的两个点 `i` 和 `i+1` 属于不同的连通分量（即 `find(i) != find(i+1)`），我们就在这两个分量对应的节点之间连一条边，权重为 1。
   - **求解**：问题就变成了，在分量图上，从 `s` 所在的分量走到 `t` 所在的分量，最少需要经过几条边。这是一个典型的无权图最短路问题，可以使用**广度优先搜索 (BFS)** 来解决。

# C++ 代码

```cpp
#include <iostream>
#include <vector>
#include <numeric>   // std::iota
#include <algorithm> // std::swap, std::min, std::max
#include <utility>   // std::pair
#include <map>
#include <queue>

// --------  DSU 模板 --------
class DSU
{
public:
    vector<int> parent;
    vector<int> sz; // 按大小合并的依据 (避免与C++的size()函数重名，改为sz)
    int count;           // 联通分量
    DSU(int n)
    {
        count = n;
        parent.resize(n);
        sz.resize(n);
        std::iota(parent.begin(), parent.end(), 0); // 从0开始连续填充
        sz.assign(n, 1);
    }
    int find(int i)
    {
        if (parent[i] == i)
            return i;
        return parent[i] = find(parent[i]);
    }
    void unite(int a, int b)
    {
        int root_a = find(a), root_b = find(b);
        if (root_a != root_b)
        {
            if (sz[root_a] < sz[root_b])
                std::swap(root_a, root_b);
            // a是大树，b合并到a
            parent[root_b] = root_a;
            sz[root_a] += sz[root_b];
            count--;
        }
    }
    bool is_connected(int a, int b)
    {
        return find(a) == find(b);
    }
    // 获取联通分量
    int get_count() const
    {
        return count;
    }
    // 获取i所在集合的大小
    int get_size(int i)
    {
        return sz[find(i)];
    }
};
// -------- DSU 模板结束 --------


int main()
{
    // C++ 标准输入输出加速
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(NULL);

    int L, m, q;
    std::cin >> L >> m >> q;

    // --- 步骤 1: 预处理，构建零费用连通分量 ---

    // DSU对象，大小为L+1以方便使用1-based索引
    DSU dsu(L + 1);

    vector<std::pair<int, int>> chords;
    for (int i = 0; i < m; ++i)
    {
        int u, v;
        std::cin >> u >> v;
        // 存储弦，并保证端点有序，方便后续判断
        chords.push_back({std::min(u, v), std::max(u, v)});
        // 合并弦的两个端点
        dsu.unite(u, v);
    }

    // 检查所有弦的配对，看它们是否相交 (O(m^2))
    for (int i = 0; i < m; ++i)
    {
        for (int j = i + 1; j < m; ++j)
        {
            int u1 = chords[i].first;
            int v1 = chords[i].second;
            int u2 = chords[j].first;
            int v2 = chords[j].second;

            // 判断相交：端点是否交错排列
            // (u1 < u2 < v1 < v2) 或 (u2 < u1 < v2 < v1)
            if ((u1 < u2 && u2 < v1 && v1 < v2) || (u2 < u1 && u1 < v2 && v2 < v1))
            {
                // 如果相交，合并它们所在的集合
                // 只需要合并任意两个不同弦上的点即可
                dsu.unite(u1, u2);
            }
        }
    }

    // --- 步骤 2: 构建“分量图” ---

    // 使用 map 将 DSU 的根节点映射到从 0 开始的连续索引
    std::map<int, int> comp_map;
    int comp_idx_counter = 0;
    for (int i = 1; i <= L; ++i) {
        int root = dsu.find(i);
        if (comp_map.find(root) == comp_map.end()) {
            comp_map[root] = comp_idx_counter++;
        }
    }

    int num_components = comp_map.size();
    vector<vector<int>> comp_adj(num_components);

    // 遍历圆周上的所有相邻点对，构建分量图的邻接表
    for (int i = 1; i <= L; ++i)
    {
        int p1 = i;
        int p2 = (i == L) ? 1 : i + 1; // p2是p1在圆上的下一个点

        // 如果相邻点属于不同分量，则在分量图上添加一条边
        if (!dsu.is_connected(p1, p2))
        {
            int root1 = dsu.find(p1);
            int root2 = dsu.find(p2);
            int idx1 = comp_map[root1];
            int idx2 = comp_map[root2];
            comp_adj[idx1].push_back(idx2);
            comp_adj[idx2].push_back(idx1);
        }
    }

    // --- 步骤 3: 处理查询 ---
    for (int i = 0; i < q; ++i)
    {
        int s, t;
        std::cin >> s >> t;

        // 如果起点和终点在同一个分量，费用为0
        if (dsu.is_connected(s, t))
        {
            std::cout << 0 << "\n";
            continue;
        }

        // 否则，在分量图上运行BFS
        int start_comp_idx = comp_map[dsu.find(s)];
        int end_comp_idx = comp_map[dsu.find(t)];

        std::queue<std::pair<int, int>> bfs_q; // 存储 {当前分量索引, 距离}
        vector<int> dist(num_components, -1); // -1表示未访问

        bfs_q.push({start_comp_idx, 0});
        dist[start_comp_idx] = 0;

        while (!bfs_q.empty())
        {
            auto [curr_comp, d] = bfs_q.front();
            bfs_q.pop();

            if (curr_comp == end_comp_idx)
            {
                std::cout << d << "\n";
                break;
            }

            for (int neighbor_comp : comp_adj[curr_comp])
            {
                if (dist[neighbor_comp] == -1) // 如果邻居未被访问
                {
                    dist[neighbor_comp] = d + 1;
                    bfs_q.push({neighbor_comp, d + 1});
                }
            }
        }
    }

    return 0;
}
```