diff --git a/content/post/算法题/nju01.md b/content/post/算法题/nju01.md
index aad9c3c..7d0d20e 100644
--- a/content/post/算法题/nju01.md
+++ b/content/post/算法题/nju01.md
@@ -2,6 +2,7 @@
title: 南软/智软2025年开放日机试第1题
description: 南京大学软件学院/智能软件与工程学院开放日机试第1题,图论+并查集问题
date: 2025-07-27T11:59:00+08:00
+lastmod: 2025-07-28T22:19:00+08:00
slug: nju01
# image: helena-hertz-wWZzXlDpMog-unsplash.jpg
categories:
@@ -25,6 +26,8 @@ math: true
- 接下来输入q行,每行两个整数,表示q个问题。如“1 2”则表示一个问题,表示点1和2之间的最少交通费。
- 程序的输出为q行,每行为一个问题的答案。
+注:题中 L 最大为 3 × 10^8
+
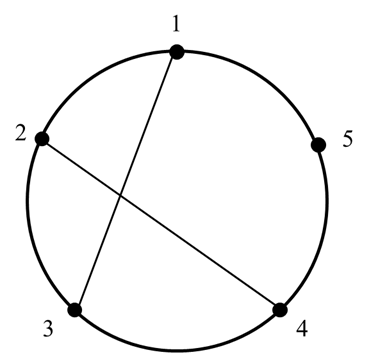 ## 示例输入
@@ -79,9 +82,9 @@ math: true
```cpp
#include
#include
-#include // std::iota
-#include // std::swap, std::min, std::max
-#include // std::pair
+#include // iota
+#include // swap, min, max
+#include // pair
#include
## 示例输入
@@ -79,9 +82,9 @@ math: true
```cpp
#include
#include
-#include // std::iota
-#include // std::swap, std::min, std::max
-#include // std::pair
+#include // iota
+#include // swap, min, max
+#include // pair
#include  ## 示例输入
@@ -79,9 +82,9 @@ math: true
```cpp
#include
## 示例输入
@@ -79,9 +82,9 @@ math: true
```cpp
#include